Simulador dos movimentos do Sol

Na página Astronomy Education at the University of Nebraska-Lincoln (aqui) está disponível um simulador dos movimentos do Sol muito completo. Vale a pena conferir.

Tristeza - Desta vez perdemos uma companheira fiel

Em menos de 6 meses se repete um dia de grande tristeza para toda a família. Perdemos a nossa cadela e grande companheira. Além da falta de seu companheiro que se foi há alguns meses os rins deixaram de funcionar, mesmo com as aplicações diárias de soro. Felizmente, para ela, foi um processo rápido e, consequentemente, de pouco sofrimento.

Foram mais de 14 anos de companheirismo e amizade desta linda cadelinha para com todos os membros da família.

Sentiremos saudades.

Outros visuais para a equação do tempo

Em novembro do ano passado escrevi um post sobre um novo visual para a equação do tempo proposto por Kevin Karney. Visitando os seu site recentemente me deparei com diversas novas propostas, bem como uma excelente apresentação e um video sobre o tema. Definitivamente o Kevin tem estado bastante ativo no estudo da representação gráfica de equação do tempo. Vale a pena dar uma olhada na página que ele criou (aqui).

Apenas para dar um idéia, segue algumas imagens.

Single Fold - Cartesian

Double Fold - Cartesian

Double Fold - Intrinsic

Polar Normal

Polar Intrinsic

Tristeza - Perdemos um grande amigo

Hoje é um dia de grande tristeza para toda a família. Perdemos o nosso cão, e grande amigo, 4 dias antes dele completar 16 anos (22/06/2011). Felizmente, para ele, foi um processo rápido - menos de 2 semanas - e, consequentemente, de pouco sofrimento. Infelizmente o câncer, que forçou a retirada de metade de sua mandíbula inferior no ano passado, voltou. Além disso, seus rins colapsaram.

Foram quase 16 anos de companheirismo e amizade para com todos os membros da família.

Sentiremos saudades.

Parque Cientec/USP - Relógio com 5 faces

Em outubro de 2005 em uma visita ao Parque Cientec da USP com os escoteiros do GE Nove de Julho - 25SP encontrei um belo relógio de sol com 5 faces (superior, Norte, Sul, Leste e Oeste). Como o tempo da visita era curto e tinha que ficar de olho nos jovens, marquei uma nova visita com o Prof. Inácio, então responsável pelas instalações.

No dia 19 de novembro o Prof. Inácio gentilmente me permitiu o acesso ao Parque para que eu pudesse fotografar e medir cada uma das faces. Munido de minha Kodak EasyShare CX4230 2.0 MPixels, réguas metálicas, esquadros, folhas de papel A3, nível, prumo, GPS, etc. comecei a registrar as características. Como o Prof. tinha outros compromissos tive 2 horas para tudo. Todas as fotos foram feitas entre as 10:00 h e 12:00 h.

De acordo com o Prof. Inácio este relógio data do final do século XIX e seu primeiro lar foi a Avenida Paulista. Após algum tempo o mesmo foi transferido para a Estação da Luz e posteriormente para o Parque Cientec. Infelizmente as datas e as localizações exatas são desconhecidas, bem como o seu idealizador e construtor.

As medições efetuadas nas linhas horárias da face Sul (vide foto abaixo) confirmam que o relógio foi desenhado para a latitude da cidade de São Paulo.

O relógio encontra-se em péssimas condições de preservação e merecia ser restaurado, ou preservado ao abrigo das intempéries e uma réplica colocada em seu lugar.

Quem sabe no futuro o Parque se interesse em restaurá-lo e resgatar a sua história e faça com que ele seja parte integrante das atrações educativas do local.

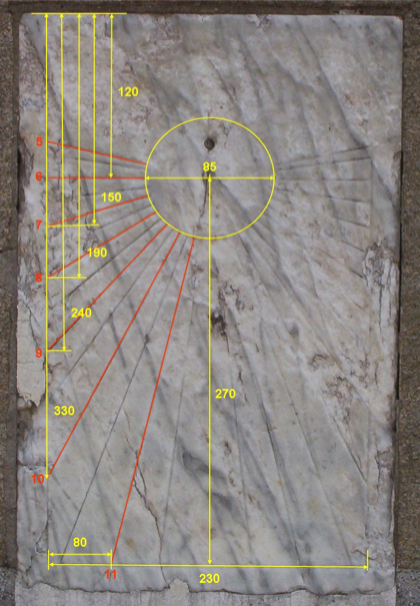
Face Sul com as linhas horárias marcadas (dimensões em milímetros)

Um novo visual para a equação do tempo

Em 28/09/2010 Kevin Karney enviou para a SML (Sundial Mailing List) a mensagem, que reproduzo abaixo, descrevendo uma nova forma de desenhar a equação do tempo, que foge da tradicional curva com forma de "8". Vale a pena considerar este tipo de enfoque quando se desejar um aspecto mais artístico.

Dear Colleagues,

You may be interested in the attached chart of the Equation of Time for 2011. It is of interest for a number of reasons...

• It is an 'intrinsic' plot - not the familiar cartesian, polar or analemmatic form. An intrinsic plot has equal increments of the independent variable along the curve of the plot rather than along the x-axis. This allows the curve to be folded - making a very compact form.


• It is much easier to read than a normal plot, because the day points are all equally spaced along the curve.


• It looks good !

The use of an intrinsic plot for the equation of time was first used in the Bury St Edmunds dial in the 1860s. See F. Sawyer: ‘The Bury St Edmunds Curve’, NASS Compendium 12(3), p.29 (Sept 2005) or John Davies: 'More on the Equation of Time on Sundials', BSS Bull 17(ii), p.75 (June 2005).

This particular 'Flame' form is one of many possible compact folded forms that can easily be generated with a spreadsheet.

For the number-obsessed, the chart is very precise. Though you cannot of course read it on the chart, the values of EoT are exact to within a fraction of a second, since I have used the 2011 polynomial algorithms issued to surveyors and navigators by HM Nautical Almanac Office. The chart is for noon UT. If anyone would like a copy - correct for their own time zone and longitude - please let me know. Or if you are familiar with Excel, you can download the spreadsheet used to draw the curve from www.precisedirections.co.uk/Sundials/Index.html. The file is called "Almanac 2010_2011.xls". This has all the polynomial coefficients for the Sun and navigational stars for both 2010 and 2011. You can see a number of other intrinsic plots of the EoT at the above website. Click on the 'Grange-over-Sands Conference' link.

For the really observant, you will notice a tiny additional gap between 31 Dec and 1st Jan: that is there because there are 365 1/4 days in a year not 365...

The zodiac signs on the chart mark the day starting the astronomical constellations when the Sun's longitude are passes 30, 60, 90 degrees etc. This may not conform with the astrological dates.

Best regards

Kevin

Relógio de sol "Analemático Digital"

Recentemente Chris Dobbie apresentou um layout interessante para um relógio de sol, que ele chama de "Analemático Digital". Em que pese o nome não seja o mais apropriado, pelas razões que veremos a seguir, a concepção abre algumas possibilidades, como: a inclusão da equação do tempo e a possibilidade de ler as horas após as 18:00 e antes das 6:00, onde a latitude assim o permita.

Os comentários quanto ao nome foram feitos pelo belga Willy Leenders cujo site pode ser acessado aqui.

1. Analemático

Um relógio de sol não é analemático apenas pelo fato de conter a analema (figura em forma de 8), que mostra a relação entre a data (declinação do Sol) e a Equação do Tempo.

Um relógio analemático usualmente tem uma face horizontal com forma elíptica, onde estão marcadas as horas; sendo que, o eixo maior fica na direção Leste-Oeste, e uma linha com as datas fica sobre o eixo menor, que fica na direção Norte-Sul. Sobre a data correta é posicionado um gnômon cuja sombra intercepta a elipse, e na hora pode ser determinada.

O termo analema vem do grego 'ana lemma', que significa visto de cima.

O relógio de sol analemática é uma projeção vista de cima de um relógio equatorial.

​

Não sei se o Chris já construiu um, mas assim que conseguir mais detalhes escreverei mais a respeito.

Parabéns Chris pela criatividade.

Como os relógios de sol funcionam - por Tony Moss - parte 4/4

Esta apresentação foi criada por Tony Moss membro da BSS (British Sundial Society). O texto e as ilustrações são propriedade intelectual do autor, que a disponibilizou para fins educacionais para os membros da BSS. A tradução para o português é de responsabilidade do responsável por este blog (Ricardo Cernic) e a sua publicação foi gentilmente autorizada pelo autor e pela BSS (licença geral).

Devido ao extenso conteúdo da apresentação a mesma foi dividida em 4 posts de forma a facilitar a leitura e o entendimento.

___________________________

Gráfico da equação do tempo

​

Diagrama da órbita anual da Terra ao redor do Sol (fora de escala)

Se a Terra ficasse parada na mesma posição e só rodasse em torno de um eixo vertical* então todos os dias teriam a mesma duração. Quando olhamos para o Sol, o estamos observando a partir de uma plataforma móvel. É a velocidade variando em torno de sua órbita elíptica e o eixo inclinado que são responsáveis pelas variações diárias contabilizados pela Equação do Tempo.

(*) Impossível, é claro, como é o movimento orbital que impede a Terra de ser arrastada para dentro pela gravidade do Sol.

Introdução aos declinantes

Em um relógio de sol vertical apontando para o Sul verdadeiro, em um muro Leste/Oeste, a linha do meio-dia é central e as linhas horárias estão dispostas simetricamente. As horas começam às 6:00 e terminam às 18:00

Relógios de sol em paredes que fazem um ângulo com a linha Leste/Oeste verdadeira são chamados de declinantes.

Na maioria dos casos a linha do meio-dia ainda será vertical, porém o ponteiro estará rotacionado de forma a continuar alinhado com o eixo da Terra.

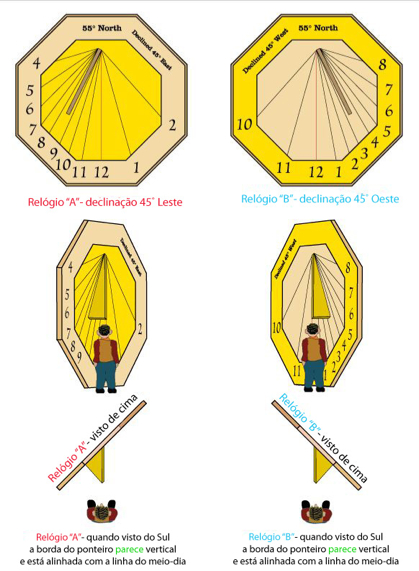
Paredes declinadas a Leste e a Oeste

Exemplos de relógios de sol

A seguir alguns exemplos de relógios de sol. A legenda está acima de cada figura.

Relógio de sol horizontal com gráfico de equação do tempo

Relógio vertical declinante 54° 20' N, 1° 26' O. Declinação 14° Leste

Relógio equatorial universal - ajustável para qualquer latitude

(face das horas de verão no hemisfério Norte)

(face das horas de inverno no hemisfério Norte)

Relógio polar com abas inclinadas para mostrar as horas de 6:00 às 18:00

(relógios polares planos não podem mostrar as primeiras nem as últimas horas do dia)

Relógio equinocial - escultor Henry Moore - Adler Planetarium, Chicago

(obstruções removidas digitalmente)

Relógio de sol analemático

(se o usuário ficar em pé, no painel central, sobre a data corrente, a sua sombra mostrará a hora solar)

(detalhe do painel com a linha de data)

Relógio de sol poliédrico

(Vinte faces triangulares equilaterais com diversos relógios declinantes e "reclinantes" - não verticais - em cada face)

Relógio horizontal portátil

Heliocronômetro

(converte a hora solar em hora civil - dos relógios comuns)

Nesta réplica de um Duplo Horizontal os ponteiros: inclinado e vertical indicam a hora solar, a hora lunar; bem como, a altitude e o azimute do Sol

Capuccino

a escala se parece com um capuz de monge

This ugly plastic ‘non-dial’ does nothing at all except display the ‘designer’s

ignorance and persuade the general public that ‘real’ sundials don’t work.

___________________________

Tony Moss (1938 - ) - professor universitário aposentado com muitos anos de experiência em trabalhos com madeira, plástico e metais. A aventura com relógios de sol começou há cerca de 20 anos, quando um amigo pediu ajuda para construir um relógio em bronze em base a um modelo de papel. Desde então projeta e fabrica relógios de sol. Ele é o dono da Lindisfarne Sundials que fabrica relógios de sol para qualquer localidade. Desde 1995 é membro da BSS - British Sundial Society.

© 2010 by British Sundial Society

© 2009, 2010 by Tony Moss

© 2010 Ricardo Cernic - relogiosdesol.blogspot.com - tradução para o português

Como os relógios de sol funcionam - por Tony Moss - parte 3/4

Esta apresentação foi criada por Tony Moss membro da BSS (British Sundial Society). O texto e as ilustrações são propriedade intelectual do autor, que a disponibilizou para fins educacionais para os membros da BSS. A tradução para o português é de responsabilidade do responsável por este blog (Ricardo Cernic) e a sua publicação foi gentilmente autorizada pelo autor e pela BSS (licença geral).

Devido ao extenso conteúdo da apresentação a mesma foi dividida em 4 posts de forma a facilitar a leitura e o entendimento.

___________________________

Relógios horizontais em latitudes diferentes

Tempo solar, correção da longitude e tempo médio de Greenwich (Inglaterra)

O Sol leva quatro minutos para percorrer um grau de longitude de Leste para Oeste.

Todos os relógios de sol na mesma linha de longitude indicam o mesmo horário (como mostrado nos relógios da figura abaixo para maior clareza).

Relógios de sol no meridiano 4° a Oeste estão 16 minutos atrasados em relação do horário de Greenwich e os que estão 8º a Oeste estão 32 minutos atrasados.

 

Exemplo: Plymouth está 4° 08' a Oeste de Greenwich. Os relógios de sol em Plymouth estão sempre 16 minutos e 32 segundos atrasados.

 

Em 1880, para evitar o caos quando as primeiras ferrovias permitiram viagens rápidas de Oeste a Leste, o Parlamento estabeleceu o horário médio de Greenwich - Greenwich Mean Time (GMT), de forma que todos os relógios do Reino Unido passaram a indicar o mesmo horário do Big Ben.

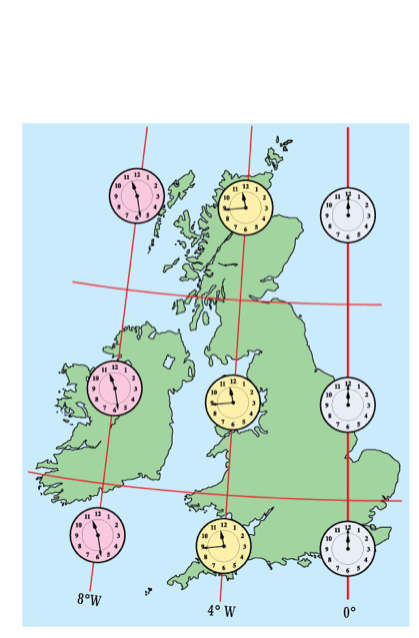
Introdução à analema

O primeiro relógio mecânico preciso foi feito em 1656 pelo cientista alemão Christian Huygens. Os seus últimos modelos tinham uma precisão de um segundo por dia. Se ele ajustou o relógio diariamente de acordo com um relógio de sol ele pode, inicialmente, ter pensado que o seu relógio variava de precisão em diferentes épocas do ano, quando de fato era o relógio que estava certo e o relógio de sol que estava variando.

Agora sabemos que todos os relógios estão fora de compasso com os relógios de sol, porque o comprimento dos dias, medido de acordo com o Sol, aumenta de alguns segundos durante um período de 3 meses para depois diminuir em quantidades similares durante os próximos 3 meses, para depois repetir o processo na metade do ano seguinte. A seguir podemos ver o que está realmente acontecendo.

A analema

Se você tirar uma fotografia no mesmo pedaço de filme (fotograma) com 10 dias de intervalo exatamente às 12:00 h do seu relógio você poderia esperar ver alguma coisa como a figura a baixo.

A equação do tempo

A figura em forma de 8 é o que aparecerá no filme após a revelação. Esta figura é chamada de “analema”.

A diferença entre a hora solar e a hora legal (a do relógios comuns) é conhecida como a “Equação do Tempo”.

Para fins práticos necessitamos de uma tabela diária com as correções em minutos e segundos para o relógio de sol ou um gráfico do qual os ajustes diários podem ser deduzidos.

___________________________

Tony Moss (1938 - ) - professor universitário aposentado com muitos anos de experiência em trabalhos com madeira, plástico e metais. A aventura com relógios de sol começou há cerca de 20 anos, quando um amigo pediu ajuda para construir um relógio em bronze em base a um modelo de papel. Desde então projeta e fabrica relógios de sol. Ele é o dono da Lindisfarne Sundials que fabrica relógios de sol para qualquer localidade. Desde 1995 é membro da BSS - British Sundial Society.

© 2010 by British Sundial Society

© 2009, 2010 by Tony Moss

© 2010 Ricardo Cernic - relogiosdesol.blogspot.com - tradução para o português

Horizontal em Itatiba - SP

Finalmente consegui, após diversos meses, concluir o relógio horizontal para um amigo médico que tem uma casa de campo em Itatiba - SP. Todos os cálculos foram feitos para as coordenadas 22 56' S - 046 43' O e foi utilizada uma placa de ardósia de 80 x 80 cm com 1 cm de espessura.

Como este meu amigo é apaixonado por cavalos gravei em baixo relevo o de desenho de um no ponteiro. A gravação química no latão do ponteiro e na placa com a equação do tempo foi feita por um amigo que trabalha em uma empresa de brindes e esculturas.

O mote utilizado foi:

DISCE • VT • SEMPER • VICTVRVS

aprenda como se fosse viver para sempre

VIVE • VT • CRAS • MORITVRVS

viva como se fosse morrer amanhã

Toda a gravação na pedra foi feita com os cinzéis feitos com brocas de vídea, que descrevi em um post anterior, e com uma microretífica com fresa diamantada. O meu filho mais novo, como sempre, ajudou na execução. O relógio instalado em seu lugar definitivo pode ser visto na figura abaixo.

​